Soluciones 2: Presión de vapor

 Cambios en la presión de vapor

Recordemos que la presión de vapor es la presión ejercida por las moléculas de un líquido que pasan a fase de vapor. 

De acuerdo a la Ley de Raoult: “El descenso relativo de la presión de vapor del disolvente es igual a la fracción molar del soluto en la solución”. Descrito de manera matemática:

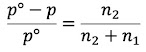
que si se arregla quedaría como:

 .......... (Ecuación 1)

Donde x1= fracción molar del solvente (número de moles de solvente, sobre la suma de moles de todos los componentes de la solución), p es la presión parcial del disolvente. Recordemos que se le llama presión parcial porque sería la presión de la fase de vapor debida al solvente. De acuerdo a la Ley de Dalton de las presiones parciales, la presión de vapor de una solución es igual a la suma de las presiones parciales de todos los componentes. Hablamos de la presión parcial cuando solo nos referimos a la que corresponde de un componente.

La Ley de Raoult implica que la presión de vapor del disolvente sobre una solución es igual a la presión de vapor del disolvente puro pº multiplicada por la fracción molar del disolvente en dicha solución. De esta manera un solvente ideal obedece la ley de Raoult en todo el intervalo de concentraciones:

En contraste, si uno de los solutos es un gas, su solubilidad está determinada por la presión parcial del gas. en la fase gaseosa o de vapor. De hecho, de acuerdo a la Ley de Henry, la masa de gas disuelta en un determinado volumen es proporcional a la presión parcial del gas en equilibrio. 

Esa proporcionalidad se puede establecer con una constante de proporcionalidad K. Así, la ecuación quedaría como:

De esta manera, se puede cambiar la presión de vapor tanto del solvente como la del soluto cambiando la concentración de este último en la solución.

En una solución ideal, la presión de vapor del solvente y del soluto siguen ambas leyes de Raoult y de Henry, de la misma manera en la que un gas idean se comporta según la ley general de los gases. Pero, en una solución ideal, la Energía libre de Gibbs no posee contribución entálpica, es decir, la entalpía molar de un componente en el líquido es igual a la entalpía molar del componente líquido puro. Dicho de otra manera, No se desprende ni se absorbe calor durante la formación de una solución líquida ideal. 

De esta manera, el potencial químico del disolvente en la fase líquida será igual a su potencial en la fase de vapor:

μlíquido=μvapor

y dado que la fase gaseosa sigue la ley general de los gases:

Si se aplica la ecuación 1 (ley de Raoult), entonces tenemos que:

Y arreglando la ecuación, nos queda:

y si hacemos , esto es, considerar el potencial químico del disolvente * igual al potencial químico del vapor + el factor de la presión, entonces

Entonces cuando el solvente esté puro (su fracción molar x1=1),  μ* será igual a μº. Así que, μ* es el potencial químico del disolvente en la fase líquida cuando se encuentra en estado puro. De manera similar se podría definir para el soluto: μ* como el potencial químico del soluto en la fase líquida cuando el soluto se encuentra puro  (un concepto abstracto, pero útil).

Eso significa que se puede reducir la presión de vapor del disolvente con el incremento en la concentración (fracción molar) del soluto, es decir, cuando se reduce la fracción molar del disolvente. De ahí que es una propiedad coligativa.

Sin embargo, eso en condiciones reales, puede desviarse del comportamiento ideal:

¿Recuerdas qué utilizamos para obtener una aproximación a los comportamientos reales (ve el blog sobre actividad y potencial químico)?. Así es, la actividad. Entonces el potencial químico de un componente puede definirse con la siguiente ecuación:

Esta ecuación permite entender los cambios en potencial químico con los cambios de concentración en condiciones reales, aún cuando la solución no sea ideal.

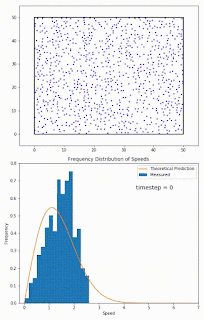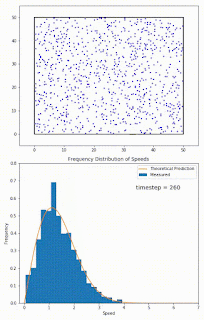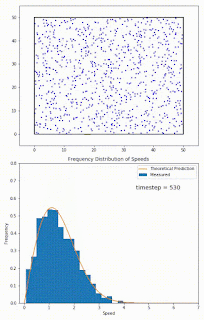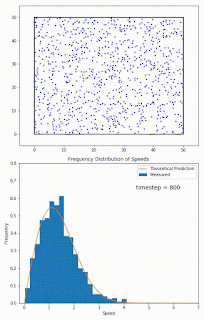
Recuerda que las moléculas en la fase líquida no tienen todas la misma energía al mismo tiempo. La energía de las moléculas tiene una distribución normal (de hecho se llama distribución Boltzmann-Maxwell) que se parece a la distribución gaussiana que viste en estadística. Y su energía puede subir o bajar, debido a su transferencia energética con otras partículas, SIN QUE HAYA INTERCAMBIO DE CALOR fuera del sistema. Estos cambios en energía se pueden ver como cambios en la velocidad. Ve el siguiente gif:

Abajo, en el eje x, está la energía, y en el eje y, el número de partículas (de hecho ponen el porcentaje). Nota como con el tiempo, las energías de cada partícula o molécula cambia, pero la energía total del sistema no cambia. Es decir, no hay ingreso o liberación de calor. Las moléculas que tienen más energía son pocas (se ven en la "cola" del lado derecho de la distribución). Estas pueden pasar a la fase vapor, y son estas las que implicarán el equilibrio con la fase gaseosa y la presión en la fase gaseosa o vapor. 

Como solo es una proporción la que tiene la energía suficiente, de ahí que solo una proporción pasa a la fase gaseosa. Si el número de moléculas o partículas cambia, también el número de moléculas que pasen a la fase gaseosa cambia de manera proporcional. Y por eso, la proporción en la fase líquida se relaciona con la proporción en la fase gaseosa, de ahí que las leyes de Raoult y Henry hablan de esta proporcionalidad.

Esta aproximación molecular de la energía cinética en un gas o líquido y su distribución dio paso a un gran avance científico, pues muchas propiedades macroscópicas pueden entenderse como el resultado de este "promedio" de la distribución energética de la partícula. De ahí que, este concepto fue madre de la Mecánica estadística actual. Esta aproximación Boltzmanniana permite entender y acercarnos a los comportamientos reales, como lo veremos más adelante. De hecho, la entropía de Boltzmann, permite entender los diferentes estados en un conjunto de moléculas. Este concepto tiene aplicaciones físicas, como el número configuraciones de partículas, biofísicas como el número de configuraciones de una proteína, hasta ecológicas como los cambios en el número de especies que pueden ser observadas con el índice Shanon-Weaver gracias a los conceptos de entropía de la información, que actualmente se usan en modelos Big-Data. Recuerda, las ecuaciones que ves, no son para verlas, sino para entenderlas y aplicarlas, son herramientas que nos sirven para entender la naturaleza.

Aplicando esto mismo, en las energías de las partículas en fase líquida, notarás que si se cambia la temperatura (recuerda que la temperatura es un promedio de la energía cinética de las moléculas, ve este blog: BioenergéticaI), el número de moléculas que pasan a la fase gaseosa también puede cambiar. Con este cambio en la presión del gas causada por el número de moléculas de soluto, también se afectará las temperaturas de ebullición y de fusión como se mencionará en la página Soluciones 3: Crioscopía y Ebulloscopía.