Previamente en el blog de acidez vimos las condiciones en que se trabaja con un amortiguador.
Recuerda ver esta página para ver cómo se calcula el valor del pH para un ácido o una base.
Recordemos que para un ácido que se disocia parcialmente (ácido débil o media fuerza):
ácido <-----> base + H+
Su constante de equilibrio, llamada Ka es
aplicando -log:
para obtener pH en función de pK, con la ecuación de Henderson-Hasselbach:De esta manera, si despejamos la relación base/ácido, nos quedaría:
A esta relación la llamamos λ.
Porcentaje de disociación
Para saber la fracción de un ácido que se ha disociado, dicha fracción la llamaremos alfa:
Simplificando,

Así, podemos graficar, la fracción de ácido que se ha disociado según el pH. Grafiquemos un ejemplo para el ácido acético pK 4.7.
Capacidad amortiguadora
Para saber qué tanto de ácido o base podemos agregar a una solución amortiguadora, se considera el valor β que es la concentración de ácido o base que se puede agregar a una solución amortiguadora cuya concentración es C para provocar un cambio de pH que simbolizamos como ΔpH. Donde C es la suma de la concentración del ácido como de la base.
Así β=[dB]/dpH=concentración de ácido en función del cambio de pH
La función es:
Con esto podemos graficar la capacidad amortiguadora en función del pH. Esto implica que depende del pH del que inicies, de ahí que se λ se calcula a partir del pH en que se encuentra el amortiguador y β es la concentración de ácido/base que se puede agregar. Usuando el mismo ejemplo de ácido acético
Se puede notar que la mayor capacidad amortiguadora se encuentra cerca del pK (4.7) +- 1 unidad de pH, es decir, la mayor capacidad amortiguadora está entre 3.7 y 5.7.
Si consideramos que usualmente β se calcula para un ΔpH de 1 (para cambiar en 1 unidad de pH la solución), el cálculo se simplifica, y la Ecuación 1 se convierte en:

Si además la solución se encuentra a un pH = pK, la capacidad amortiguadora es la máxima, es decir que la máxima concentración de ácido que se puede agregar es:
β=(9/22)C.
Por ejemplo, para una solución 1 M de ácido acético, la máxima concentración de ácido que se puede agregar para que el pH no cambie más de 1 sería (9/22)(1)=0.41 M
Si la concentración de ácido acético fuera menor, digamos 20 mM, entonces la máxima concentración de ácido que se puede agregar es 8.2 mM
Quiz: ¿Cuál debería ser la concentración de acético para no permitir un cambio mayor a 1 pH cuando se agreguen 10 mM de ácido si la solución está a pH 4.7?
Quiz: ¿Cuál debería ser la concentración de buffer de acetatos para no permitir un cambio mayor a 1 pH cuando se agreguen 10 mM de ácido si la solución está a pH 4.2?
R: β=10 mM. Hay que calcular λ, recordemos que λ=10^(ph-pK)=10^(4.2-4.7)=0.316
R: β=10 mM. Hay que calcular λ, recordemos que λ=10^(ph-pK)=10^(4.2-4.7)=0.316
En esta condición
β=C(9*0.316)/[(1+0.316)(1+10*0.316)]=2.844*C/[1.316*4.16]=2.844*C/5.47456
β=0.519*C. Como β=10 mM, entonces: C=β/0.519=10mM/0.519=19.25 mM
La concentración del buffer de acetatos para no permitir un cambio mayor a 1 unidad de pH cuando se agreguen 10 mM de ácido si la solución está a 4.2, es de 19.25 mM del buffer de acetatos. La concentración del buffer de acetatos para mantener la solución amortiguadora entre 3.2 y 5.2 es de 19.25 mM
Si se quiere poner más estricto y no permitir un cambio ( ΔpH) mayor de 0.1 unidades de pH, entonces la ecuación 1 deviene en:
Si la solución está a un pH igual al pK, entonces β=0.0573Ce, para que el ΔpH sea de 0.1
Quiz. ¿Cuál debe ser la concentración de Tris (pK 8.06) para que, aunque se produzcan 10 mM de ácido, la solución se mantenga entre 7.96-8.16?
Para eso, se entiende que debe prepararse Tris a 8.06 y solo se permite un +/- 0.1 unidades de pH.
C=β/0.0573=10mM/0.0573= 174.52 mM. La concentración de Tris debe ser 174.52 mM a pH 8.06 para mantener el pH entre 7.96 y 8.16.

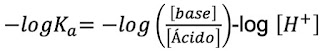
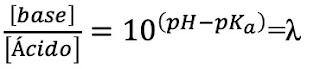





No hay comentarios:
Publicar un comentario